I came across a helpful resource last month, but am just now finding time to post. (Ah, the holidays!) This is another offering from the people at the Institute for Excellence in Writing-- aka IEW-- and I have already used it with my tutoring students as well as my Sunday morning Bible class. It's that versatile! And, no, this is not a paid or compensated endorsement.
The book is called Teaching With Games, by Lori Verstegen, and can be purchased either as a book only or as a dvd workshop course with the book and video examples of teachers using the games with actual students. I'm cheap, so I just bought the book. It has reproducible games and templates for customizing your own games, plus ideas for easy "no-prep" games. Granted, many of them are old standards like Bingo, Hangman, and Jeopardy, but having them all together, with ideas for using them in the various subjects, is very helpful for teachers like me who get stuck in a rut. It's like reading a recipe book when you find yourself making the same dinners over and over: sometimes you just need to be reminded that other meals exist.
One of the first games I tried was "Fun Times" with my math kids. It's pretty simple-- the game board is a one-page reproducible table with columns labeled 5, 6, 7, 8, 9, and 10 across the top, and rows labeled 2, 3, 4, 5, 6, 7 down the side. Within the table are the products of the numbers; e.g., where 4 and 7 intersect, the square is labeled 28, and the square where 9 and 6 intersect is labeled 54. Also, some squares are grey and others are left white. To play the game, students use two dice that have been modified so that one has the numbers 7-10 and the other has the numbers 2-7. The player rolls the dice, and multiplies the resulting numbers, placing his marker on the appropriate square on the board. The second player then goes. If he rolls a number that has already been played, he can replace it with his own marker if it is not a gray "safe" square. The object of the game is to get four squares in a row (like Bingo, in any direction). Any markers can be used-- I used pennies and covered half of them with pieces of paper to distinguish the two players. The game is easy, fast, and my students enjoy it more than regular multiplication drills.
My Bible class has also recently played Jeopardy and Wheel of Fortune as suggested in the book. They loved both, and for Jeopardy I was able to reuse game cards I had made for a previous board game that we had all grown tired of. Funny how a different format can renew their excitement over old material!
A blog devoted to making math concepts, reading, spelling and writing skills accessible to K-8 students through hands-on activities.
Friday, December 4, 2015
Monday, October 19, 2015
A Spoon Full of Sugar
The song goes, "In every job that must be done there is an element of fun." Well, sometimes a student's job can be so frustrating that you might want to try to make the fun a little more obvious. This post was inspired by one of my students who needed some fun added to his daily dose of math word problems.
I needed a quick, simple, one-player game that would give him an immediate reward for answering a solving a word problem correctly. It had to be fairly quick to play, because I planned to use it as part of our tutoring session. I also needed to have the answers available from a neutral source (so it wouldn't be me telling him if he was wrong), and there needed to be some kind of variability in the score-- partly skill, partly chance, to add interest. If he got the same score every time that would be kind of pointless.
So, here's how the game is played:
I needed a quick, simple, one-player game that would give him an immediate reward for answering a solving a word problem correctly. It had to be fairly quick to play, because I planned to use it as part of our tutoring session. I also needed to have the answers available from a neutral source (so it wouldn't be me telling him if he was wrong), and there needed to be some kind of variability in the score-- partly skill, partly chance, to add interest. If he got the same score every time that would be kind of pointless.
 |
| Left to right: Orange-covered answer key with two game cards on top, word problem side up; white game board with cards and game pieces; bottom: extra cards and game pieces. |
This particular game is done with a Pokémon theme, but can be translated into just about anything the student is interested in. The basic idea is that the student must answer a question correctly to move a game piece from one circle to the other. In this case, the game pieces are Pokémon, and the player rescues them as he moves each piece from the bad guys' side to the good guys' side. Another child might respond better to a game that features puppies being moved from the animal shelter to a home, cookies moving from the cookie jar to a plate, or princesses moving from the dragon's lair to a castle. The possibilities are endless. My student likes Pokémon, so that's what I used.
My game pieces were made from a dozen milk carton caps I had saved, but anything will work-- coins, poker chips, rocks, plastic figurines, Sculpey clay creations. The caps worked well for me because they were the perfect size to glue on small round Pokémon printables that I found online. (I glued a Poké Ball picture to the top of each cap, and then a different Pokémon character inside each one.)
The game board is just a Pages (Mac word processor) creation that has the two circles, the rules, and some graphics inserted from online images. Once I had it designed and printed out, I put it into a plastic page protector. Not only does this keep the board clean, but it also allows the student to write his scores on the page using a dry erase marker.
To make the game cards, I made a template using another word processing feature: the table. I inserted a table onto a new page and set it to have four columns and two rows, adjusting the height and width of the cells to approximate a card size. Then all I had to do was find an appropriate image to go on the back of each card. I inserted the image into every other cell, and then each of in the remaining spaces, I typed one of the student's word problems (from his textbook), replacing names and details with Pokémon characters and appropriate scenarios.
 |
| This game board has a Pokémon theme, but it could be anything. |
I made 16 cards, using a total of 4 pages. After printing them out, I cut the cards out so that each blue Pokémon back could be folded over and have a word problem on the front. A bit of glue holds the two sides together, and viola! A stack of game cards.
 |
| The game card template after the back image is inserted, before the word problem is added. |
To create an answer key, I used another table insert-- but this time, the table included the question number, solution process and final answer. Each card was labeled with a letter+number to correspond with its answer on the chart. To keep the student from seeing all the answers as he's checking for one, I made a cover sleeve for the answer key with a narrow window that shows only one answer at a time. To allow the answer key to slide up and down in the sleeve, I added a paper pull strip at the top of the key.
 |
| This is the answer key chart. More problems and answers can be added later just by adding more rows to the table. |
- The student places 5 random game pieces (Poké Balls) in the bad guys' (Team Rocket’s) circle.
- The student places 5 random cards face down in the "cards" rectangle.
- The student draws a game card, reads the card and answers the question. If writing out the problem helps, that is allowed.
- The student check his answer with the Solution Chart.
- If he answered correctly, he chooses one game piece (Poké Ball) to move to the good guys' circle (Safety Zone).
- When all the cards are gone, the student tallies his points: in this case, 5 points for each regular Pokémon, 10 for Pikachu.
I specifically have the student choose only five game pieces and five cards per game, because solving five word problems are about the limit of "fun" as far as math goes-- even when Pokémon are at stake. Any more than that and I think the student would lose the thrill of the game.
If the game is made using a different theme, there needs to be a way to vary the points. This game is set up so that the student chooses look-alike Poké Balls without knowing what Pokémon are inside. Here are some other ideas:
- Hide colored beads under the caps, shell-game style, and have different point values depending on the colors of the beads. (In this case you might have to start with all the game pieces on the board and slide off the ones not selected before play begins, so that the player does not know which ones are under his chosen pieces.)
- Use a dry-erase marker to number the bottom of each game piece before the player chooses his pieces. This way, the point value for any piece can change with every game session.
It's hard to stay motivated to do your best when school days seem to bring nothing but more and more work. This particular game brought joy to my student today, and that made me happy, too!
Tuesday, October 13, 2015
Overcoming struggles with writing
Many students have trouble with writing paragraphs, let alone essays. For some, the difficulty lies in getting the ideas out of their heads and onto paper. There are too many things to think about all at once-- the ideas themselves, the words, the spelling, even the act of physically writing the letters can be an obstacle for some children. For others, the ideas are easy enough, but they tend to come out in a rambling, completely disorganized manner. Happily, both of these problems can be addressed.
For the first problem, that of expressing the ideas on paper, I have been most impressed by the techniques of Andrew Pudewa's Institute for Excellence in Writing (IEW). (And no, I have no stock in his company nor am I being compensated for mentioning it.) While some people whose children are blessed with a natural talent for writing might cringe at his methods and call them "formulaic" (or worse), there is a definite population of students who benefit from his carefully incremental approach. The child who sits and cries over his writing assignments, for whom writing three sentences is like pulling teeth, will find IEW a relief.
The problem for these students is that converting their thoughts into words feels like a Herculean task. They can speak just fine, but somehow slowing their brain down enough to translate thoughts into written sentences is near impossible. So IEW takes a step back, and has students first translate someone else's ideas into sentences. They begin by reading short paragraphs and making a "key word outline," choosing two or three of the most important words from each sentence. The student then creates a new sentence for each set of words. (In effect, he is also learning to take notes without plagiarizing!) Here is an example, using the paragraph I wrote above as the original text:
Of course, the vocabulary in my original paragraph is not suited to a young reader or writer, but I hope you get the idea. Once the student has had practice with writing key word outlines and turning them into new paragraphs, he is introduced to the idea of writing key word outlines from the information in his own head. The student is then not overwhelmed, because he is able to get all of his ideas down, a few words at a time, before going back to construct complete sentences. When this process has become easy, the student begins to add complexity to his sentences by adding "dress-ups," such as introductory phrases, precise nouns, verbs, adverbs and adjectives, and various sentence constructions.
Some students have no trouble at all writing complete sentences, but need help organizing them into a coherent paragraph. They may be used to typing away on a computer, and think creating an outline is an unnecessary step. The result is a disorganized mess. The concept of paragraph structure doesn't register at all.
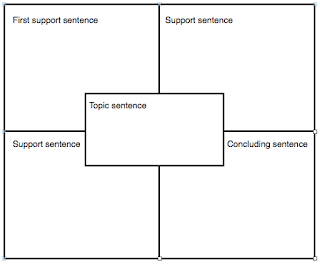
There are many graphic organizers that are helpful for this. One very effective system was developed by J.S. and E.J. Gould, called the Four-Square Writing method. (No compensation here, either.) In this method, the paragraph is visualized as a block divided into sections, so that the topic sentence, supporting ideas and conclusion are presented as a unit. This not only helps the students to remember to include each element, but also helps them understand that all of the pieces work together.
Here is one example of a Four Square graphic organizer. Note that the topic sentence bar touches each of the other sections, and all of the sections together form a single square.
While the graphic organizer may be helpful on its own, the Goulds have developed a program of sequential lessons for various ages of students that help the students understand what makes a good topic sentence, how to write good supporting sentences, and how to conclude a paragraph without simply restating the topic sentence.
Here's an example of the organizer filled out with supporting details, topic and concluding sentences.
For the record, there is "mind-mapping" software such as FreeMind or SimpleMind that will guide a student through placing sentences in a graphic organizer, and then turn these words into an outline; these may be helpful for certain students. In my experience, however, I have not seen any such programs that get across the idea of paragraph cohesion to the same degree as the simple Four Square box. Once the student understands paragraph structure, the mind-mapping may be great, but until then it's just another tool to make his ramblings more complex.
Whether your student needs help getting the words on paper or just getting the words organized, the best approach is to start where he is and proceed at a comfortable pace. Slow and steady wins the race!
For the first problem, that of expressing the ideas on paper, I have been most impressed by the techniques of Andrew Pudewa's Institute for Excellence in Writing (IEW). (And no, I have no stock in his company nor am I being compensated for mentioning it.) While some people whose children are blessed with a natural talent for writing might cringe at his methods and call them "formulaic" (or worse), there is a definite population of students who benefit from his carefully incremental approach. The child who sits and cries over his writing assignments, for whom writing three sentences is like pulling teeth, will find IEW a relief.
The problem for these students is that converting their thoughts into words feels like a Herculean task. They can speak just fine, but somehow slowing their brain down enough to translate thoughts into written sentences is near impossible. So IEW takes a step back, and has students first translate someone else's ideas into sentences. They begin by reading short paragraphs and making a "key word outline," choosing two or three of the most important words from each sentence. The student then creates a new sentence for each set of words. (In effect, he is also learning to take notes without plagiarizing!) Here is an example, using the paragraph I wrote above as the original text:
Of course, the vocabulary in my original paragraph is not suited to a young reader or writer, but I hope you get the idea. Once the student has had practice with writing key word outlines and turning them into new paragraphs, he is introduced to the idea of writing key word outlines from the information in his own head. The student is then not overwhelmed, because he is able to get all of his ideas down, a few words at a time, before going back to construct complete sentences. When this process has become easy, the student begins to add complexity to his sentences by adding "dress-ups," such as introductory phrases, precise nouns, verbs, adverbs and adjectives, and various sentence constructions.
Some students have no trouble at all writing complete sentences, but need help organizing them into a coherent paragraph. They may be used to typing away on a computer, and think creating an outline is an unnecessary step. The result is a disorganized mess. The concept of paragraph structure doesn't register at all.
There are many graphic organizers that are helpful for this. One very effective system was developed by J.S. and E.J. Gould, called the Four-Square Writing method. (No compensation here, either.) In this method, the paragraph is visualized as a block divided into sections, so that the topic sentence, supporting ideas and conclusion are presented as a unit. This not only helps the students to remember to include each element, but also helps them understand that all of the pieces work together.
Here is one example of a Four Square graphic organizer. Note that the topic sentence bar touches each of the other sections, and all of the sections together form a single square.
While the graphic organizer may be helpful on its own, the Goulds have developed a program of sequential lessons for various ages of students that help the students understand what makes a good topic sentence, how to write good supporting sentences, and how to conclude a paragraph without simply restating the topic sentence.
Here's an example of the organizer filled out with supporting details, topic and concluding sentences.
For the record, there is "mind-mapping" software such as FreeMind or SimpleMind that will guide a student through placing sentences in a graphic organizer, and then turn these words into an outline; these may be helpful for certain students. In my experience, however, I have not seen any such programs that get across the idea of paragraph cohesion to the same degree as the simple Four Square box. Once the student understands paragraph structure, the mind-mapping may be great, but until then it's just another tool to make his ramblings more complex.
Whether your student needs help getting the words on paper or just getting the words organized, the best approach is to start where he is and proceed at a comfortable pace. Slow and steady wins the race!
Saturday, October 10, 2015
A quick and effective spelling activity
This is a fun, quick and effective activity that my tutoring students enjoy as they study their weekly mutlti-syllable spelling lists. All it takes is paper, something to write with, and scissors.
First, rewrite the spelling words correctly or type them up in a fairly large font. Cut each word into a separate strip of paper. Keep the original list handy.
Now have the student use the scissors to divide the words into syllables. Help him if needed; if you're not sure where the separation should be, a dictionary with pronunciation guides will be helpful.
If a mistake is made, no problem--- a bit of tape can be used, or the word can be re-written,
and then cut correctly. Don't worry too much over
words that could possibly be divided more than one way. For example, it
is not the end of the world if the child cuts 'particle' into part i
cle instread of par ti cle. A true mistake would be "pa rti cle."
This is a good time to take notice of the various spelling patterns found in the syllables. For example, when looking at "anemone," I might remark to the student, "That last e is unusual. When I first saw that word, I thought it was a silent e, like "an-e-mone." We usually spell final e sounds with a y or ey, like "funny money." This word comes from the Greek language, though, and they don't use silent e. It's the same e we see with the spelling of Harry Potter's friend Hermione."
When the words are all cut up, scramble the syllables
and then have the student reconstruct the words as you read out the list.
With this activity, the student does not have to write the words himself, but is still using his hands and eyes to put the words together. Most importantly, however, he is focused on seeing the words in small, memorable pieces, and matching the sounds of the words to the spelling of the syllables. As I've mentioned before in other posts, this is a critical step that students often miss when they are just seeing the whole word as a string of letters.
An added benefit of this activity is that it is less likely to result in a meltdown from a tired or frustrated student, whereas a written or oral spelling practice session might be too much. Completing this "game" can be done with the student completely silent and not using a pen or pencil at all. Plus, if the pieces are kept in an envelope for future use, the student has a quick spelling review for as long as he needs.
If you allow the student to use the word pieces for independent study, be sure to include the spelling list so he can check his work. If he is likely to miss details, make the pieces self-checking by labeling the pieces of each word with a matching number or symbol. For example, "plank" and "ton" might each have a 2 on the back, so the student can check for a match by turning them over. (In case of repeated syllables, such as the "gen" in hydrogen and oxygen, you might put two symbols on both "gen" pieces.)
This activity will not solve every child's spelling problems-- and it's no help at all for beginners' one-syllable lists-- but it should be a helpful addition to word study methods.
First, rewrite the spelling words correctly or type them up in a fairly large font. Cut each word into a separate strip of paper. Keep the original list handy.
 |
| Spelling words are cut into strips. |
Now have the student use the scissors to divide the words into syllables. Help him if needed; if you're not sure where the separation should be, a dictionary with pronunciation guides will be helpful.
 |
| Each word is cut into syllables. |
This is a good time to take notice of the various spelling patterns found in the syllables. For example, when looking at "anemone," I might remark to the student, "That last e is unusual. When I first saw that word, I thought it was a silent e, like "an-e-mone." We usually spell final e sounds with a y or ey, like "funny money." This word comes from the Greek language, though, and they don't use silent e. It's the same e we see with the spelling of Harry Potter's friend Hermione."
When the words are all cut up, scramble the syllables
 |
| Syllables are mixed up. |
 |
| Words are reassembled. |
With this activity, the student does not have to write the words himself, but is still using his hands and eyes to put the words together. Most importantly, however, he is focused on seeing the words in small, memorable pieces, and matching the sounds of the words to the spelling of the syllables. As I've mentioned before in other posts, this is a critical step that students often miss when they are just seeing the whole word as a string of letters.
An added benefit of this activity is that it is less likely to result in a meltdown from a tired or frustrated student, whereas a written or oral spelling practice session might be too much. Completing this "game" can be done with the student completely silent and not using a pen or pencil at all. Plus, if the pieces are kept in an envelope for future use, the student has a quick spelling review for as long as he needs.
If you allow the student to use the word pieces for independent study, be sure to include the spelling list so he can check his work. If he is likely to miss details, make the pieces self-checking by labeling the pieces of each word with a matching number or symbol. For example, "plank" and "ton" might each have a 2 on the back, so the student can check for a match by turning them over. (In case of repeated syllables, such as the "gen" in hydrogen and oxygen, you might put two symbols on both "gen" pieces.)
This activity will not solve every child's spelling problems-- and it's no help at all for beginners' one-syllable lists-- but it should be a helpful addition to word study methods.
Tuesday, September 29, 2015
Skip-Counting Beads (Pickle Beads)
 |
| A set of 10 Skip-Counting Beads |
A set of skip-counting beads is a hands-on tool for skip-counting-- helpful not only for learning to skip-count, but also for visualizing multiplication as a concept, and comparing the quantities involved. As an added bonus, it is also a handy illustration for Least Common Multiples.
If your student is just starting out in the lower grades, it would be beneficial to have him string his own beads, perhaps one set a day. Older children might make more strings per session. Some students may lack the fine motor skills or patience to complete the set without a meltdown; it's not a total loss if you end up making them yourself, as long as the student uses them when you're finished.
 |
| Materials for making the strings. |
 |
| Bottom to top: One, Two, Three, Four, and Five strings. |
To label the beads, write the numbers 1-12 on the beads of smallest string, and then write the
 |
| Labeled beads. (Needed a finer point marker.) |
each string. (Writing the numbers on all of the white beads on every string is not a bad idea, but it may take the emphasis off the colored beads. However, some children may prefer having every bead labeled, and that's okay.)
To use the beads, the student holds a string in his hands and touches the colored beads as he counts aloud. If he needs help. he can either count up using the white beads or read the number written on the colored beads. The student should practice until he can rattle off the numbers easily.
Later, when the student is learning his multiplication tables, you can show him how it works on the string: for the 3 times table, for example, use the Three string on which every third bead is colored. Touch the first colored bead as you say, "Three times one is three." Then touch the second colored bead: "Three times two is six," and so on, up the string to "Three times twelve is 36." Then demonstrate the facts out of order: count up 5 colored beads, and say, "Three times five is fifteen." Count up nine: Three times nine is twenty-seven."
 |
| Lining up Three and Four string. |
To illustrate Least Common Multiple (LCM), explain to the student that the colored beads represent multiples of a number. When you skip count, you are listing the multiples of a number in order. To find the LCM of a pair of numbers, line up strings representing the numbers you are comparing.
 |
| Lining up Four and Five string. |
You can use the strings to show LCM of more than two numbers; just line up three or more strings together to point out the alignment of the colored beads. Five, Ten and Two align at 10; Three, Six, Two, and Nine align at 18. (Some number combinations cannot be shown given the length of the strings; for example, the LCM of 9, 5, and 10 is 90, but the Five string stops at 60.)
Once the student has mastered the use of the skip-counting beads, he is well on his way to understanding-- and mastering-- multiplication.
Thursday, September 17, 2015
Multiplying: from single- to multi-digit numbers in 10 simple steps
Multiplying large numbers by other large numbers is a process that normally is taught over several years. In second or third grade, students begin to learn the single-digit multiplication tables, and then gradually the difficulty of their calculations in increased. By sixth grade, most will be multiplying multi-digit numbers with ease.
But if you are working with a student who got a late start, or has some learning gaps and needs to catch up, you don't have "years" to work with. Happily, the older student will likely not need years. She (or he) will just need the gaps filled in and can then make quick progress. But first make sure those multiplication tables are learned, at least through the 10's.
Once your student has her math facts down pat, it's time to learn how to work with multi-digit numbers. Ready? Let's Go!
Step one: Be sure the student can visualize what it means to multiply. Use manipulatives (math rods, or beads, popsicle sticks, toothpicks, beans) to model for her, and then have her model for you, that 3 x 4 means four groups of three things, and 4 x 3 gives you the exact same product with three groups of four things. Have her show you all the 1-9 times tables until you are sure she understands what is happening.
Step two: Have her compare the 1 and 10 times tables. With the 1's, one group of one, two, six, or any other number will be that same number. With the 10's, ten times any number is the number with a zero after it. This is important. If she doesn't see it immediately, have her write down the 1's and 10's beside each other until she sees the pattern.
1x2=2 10x2=20
1x3=3 10x3=30
1x4=4 10x4=40
1x5=5 10x5=50
Step three: Have her model with manipulatives the 2's tables and then 20 times each number:
2x2=4 20x2=40
2x3=6 20x3=60
2x4=8 20x4=80
2x5=10 20x5=100
She may see the pattern before modeling. If so, have her just write out the products. Once she sees the pattern, have her tell you what 30, 40, 50, 60, etc multiplied by each digit will be.
Step four: Show her how to write the problems vertically. When she writes the answer, have her write the zero first and then the rest of the product. Tell her we write the zero first to hold the ones' place and then we can multiply the other digits-- in this case, 6 x 4:
60 60 60
x4 x4 x4
0 240
Step five: When she can quickly do problems like 40 x 6 = 240, 70 x 3 =210, 50 x 9 = 450, show her a problem like 62 x 4. How do we work this out?
All we have to do now is understand what 62 means: 60 + 2. 6 tens and 2 ones. So have her work the two parts of the equation separately: 60 x 4 = 240, and 2 x 4 = 8. Then she adds them together: 240 + 8 = 248.
Step six: Show her how to work through the multiplication in one vertical problem. 62 x 4: This time instead of writing the zero, she multiplies the 4 by the 2 and writes 8 in the one's place. Then she immediately goes back to the 4 and multiplies it by the 6. Even though it is actually 60, she doesn't need to write 240 because the 8 is holding the one's place.
62 62 62
x 4 x 4 x 4
8 248
Step seven: carrying tens.
If she is familiar with quarters and dollars, the student may already know that 25 x 4 = 100. If not, remind her that 25 means 20 + 5. 2 tens and 5 ones. So have her work the two parts of the equation separately: 20 x 4 and 5 x 4. Then she adds them together. 20 x 4 = 80, 5 x 4 = 20, 80 + 20 = 100.
But how does that work vertically? In this case, remind her that 20 means 2 tens and 0 ones. So we put zero in the one's place. Just as when we add, the 2 gets carried over to the tens' place, to be added in after we multiply 20 x 4.
So, then we try something like 67 x 4.
She should have a lot of practice with this step before going on to the next one. You can find practice problems here.
Step eight: 2 digit x 2 digit multiplication. This is similar to steps 5 and 6. Once she has 2 digit x 1 digit multiplication down, show her a 2 digit x 2 digit problem. For example, 62 x 47. Now, ask her to split up 43: 40 + 3. So now she can do two multiplication problems: 62 x 7, and 62 x 40. If she isn't sure about the 62 x 40, remind her that it's just like 62 x 4 with the "0" place holder on the end:
62 62 62
x 47 x 7 x 40
434 2480
Now she can add the products together:
434
+ 2480
2914
Step nine: 2 digit x 2 digit multiplication in one vertical problem. Step eight works, but it takes a lot of time and space. Happily, we have a short cut! We can split the numbers and still work with them one at a time, without rewriting them. And then we can add the products together without rewriting them!
The operational steps are the same-- multiply the ones, multiply the tens, then add the products. But since we know we're going to add them in our final step, we go ahead and write them that way to begin with. Emphasize the importance of using that place-holding zero in the second line to keep the digits lined up correctly.
62 62 62 62
x47 x47 x47 x47
434 434 434
2480 +2480
2914
Step ten: infinity and beyond. Your child will probably understand immediately how to do 3 digit by 1 digit (452 x 7), and then 4 digit by 1 digit (4276 x 3). Give her some practice with those. When she can do those, give her 3 digit x 2 digit (452 x 27) and 4 digit by 2 digit (4276 x 53).
Finally, introduce the idea of multiplying by 100. How many place-holding zeroes do we use? Two.
So when we have a problem in which a number is multiplied by a three-digit number, we can use our short cut with a third line for the hundreds, and use those two place-holding zeroes before adding all three rows:
162 162 162 162
x247 x247 x247 x247
1134 1134 1134
6480 6480
32400 + 32400
40014
At this point, the student should see the pattern, but if not, you can explain to her that for every digit you are multiplying the top number by, we use a separate row for the product and the appropriate number of place-holding zeroes for every row after the first product. The final answer comes from adding the individual products together, being sure to keep the numbers lined up.
With practice, this pattern will become second nature and your student will be successfully multiplying as many digits as she needs to.
But if you are working with a student who got a late start, or has some learning gaps and needs to catch up, you don't have "years" to work with. Happily, the older student will likely not need years. She (or he) will just need the gaps filled in and can then make quick progress. But first make sure those multiplication tables are learned, at least through the 10's.
Once your student has her math facts down pat, it's time to learn how to work with multi-digit numbers. Ready? Let's Go!
 |
| 4 x 3 = 3 x 4 |
Step two: Have her compare the 1 and 10 times tables. With the 1's, one group of one, two, six, or any other number will be that same number. With the 10's, ten times any number is the number with a zero after it. This is important. If she doesn't see it immediately, have her write down the 1's and 10's beside each other until she sees the pattern.
 |
| Modeling 2's and 20's |
1x2=2 10x2=20
1x3=3 10x3=30
1x4=4 10x4=40
1x5=5 10x5=50
Step three: Have her model with manipulatives the 2's tables and then 20 times each number:
2x2=4 20x2=40
2x3=6 20x3=60
2x4=8 20x4=80
2x5=10 20x5=100
She may see the pattern before modeling. If so, have her just write out the products. Once she sees the pattern, have her tell you what 30, 40, 50, 60, etc multiplied by each digit will be.
Step four: Show her how to write the problems vertically. When she writes the answer, have her write the zero first and then the rest of the product. Tell her we write the zero first to hold the ones' place and then we can multiply the other digits-- in this case, 6 x 4:
60 60 60
x4 x4 x4
0 240
Step five: When she can quickly do problems like 40 x 6 = 240, 70 x 3 =210, 50 x 9 = 450, show her a problem like 62 x 4. How do we work this out?
All we have to do now is understand what 62 means: 60 + 2. 6 tens and 2 ones. So have her work the two parts of the equation separately: 60 x 4 = 240, and 2 x 4 = 8. Then she adds them together: 240 + 8 = 248.
Step six: Show her how to work through the multiplication in one vertical problem. 62 x 4: This time instead of writing the zero, she multiplies the 4 by the 2 and writes 8 in the one's place. Then she immediately goes back to the 4 and multiplies it by the 6. Even though it is actually 60, she doesn't need to write 240 because the 8 is holding the one's place.
62 62 62
x 4 x 4 x 4
8 248
Step seven: carrying tens.
If she is familiar with quarters and dollars, the student may already know that 25 x 4 = 100. If not, remind her that 25 means 20 + 5. 2 tens and 5 ones. So have her work the two parts of the equation separately: 20 x 4 and 5 x 4. Then she adds them together. 20 x 4 = 80, 5 x 4 = 20, 80 + 20 = 100.
But how does that work vertically? In this case, remind her that 20 means 2 tens and 0 ones. So we put zero in the one's place. Just as when we add, the 2 gets carried over to the tens' place, to be added in after we multiply 20 x 4.
So, then we try something like 67 x 4.
She should have a lot of practice with this step before going on to the next one. You can find practice problems here.
Step eight: 2 digit x 2 digit multiplication. This is similar to steps 5 and 6. Once she has 2 digit x 1 digit multiplication down, show her a 2 digit x 2 digit problem. For example, 62 x 47. Now, ask her to split up 43: 40 + 3. So now she can do two multiplication problems: 62 x 7, and 62 x 40. If she isn't sure about the 62 x 40, remind her that it's just like 62 x 4 with the "0" place holder on the end:
62 62 62
x 47 x 7 x 40
434 2480
Now she can add the products together:
434
+ 2480
2914
Step nine: 2 digit x 2 digit multiplication in one vertical problem. Step eight works, but it takes a lot of time and space. Happily, we have a short cut! We can split the numbers and still work with them one at a time, without rewriting them. And then we can add the products together without rewriting them!
The operational steps are the same-- multiply the ones, multiply the tens, then add the products. But since we know we're going to add them in our final step, we go ahead and write them that way to begin with. Emphasize the importance of using that place-holding zero in the second line to keep the digits lined up correctly.
62 62 62 62
x47 x47 x47 x47
434 434 434
2480 +2480
2914
Step ten: infinity and beyond. Your child will probably understand immediately how to do 3 digit by 1 digit (452 x 7), and then 4 digit by 1 digit (4276 x 3). Give her some practice with those. When she can do those, give her 3 digit x 2 digit (452 x 27) and 4 digit by 2 digit (4276 x 53).
Finally, introduce the idea of multiplying by 100. How many place-holding zeroes do we use? Two.
So when we have a problem in which a number is multiplied by a three-digit number, we can use our short cut with a third line for the hundreds, and use those two place-holding zeroes before adding all three rows:
162 162 162 162
x247 x247 x247 x247
1134 1134 1134
6480 6480
32400 + 32400
40014
At this point, the student should see the pattern, but if not, you can explain to her that for every digit you are multiplying the top number by, we use a separate row for the product and the appropriate number of place-holding zeroes for every row after the first product. The final answer comes from adding the individual products together, being sure to keep the numbers lined up.
With practice, this pattern will become second nature and your student will be successfully multiplying as many digits as she needs to.
Tuesday, September 15, 2015
Memorizing multiplication facts
If you haven't seen Times Tales, you should check it out. It is the quickest way I know to get those multiplication facts to stick in the brains of kids who are having trouble with memorization.
But if you can't buy one more piece of curriculum, here's the system in a nutshell: turn each digit into a picture, and then combine them in scenarios that help you remember the products. If you buy Times Tales, the work is already done for you, and there are illustrations and flash cards and other helps. You can do the same thing yourself, though, with a little imagination.
For example: Draw a 5 and doodle it into a duck. Draw a 9 and turn it into a balloon with a string. Then make up a scenario, such as, "The duck had a balloon that blew away in the wind, and he chased it for 45 minutes." 5 x 9 = 45
Draw an 8 and turn it into an owl: "The owl saw the balloon stuck in a tree. He hopped across 7 branches and pecked it 2 times before it popped." 8 x 9 = 72.
Draw a 6 and make it into a mouse with a long tail. "The owl tried to catch the mouse but those 4 tiny feet ran 8 yards to his hole and he was safe," 6 x 8 = 48
Draw 7 and make it a flag. "The duck saluted the flag from 3pm to 5pm." 5 x 7 = 35
Anyway, you get the idea. You don't have to make up a story for all of them, just the ones your child finds hard to remember. If you can get your child to make up the scenarios, all the better!
But if you can't buy one more piece of curriculum, here's the system in a nutshell: turn each digit into a picture, and then combine them in scenarios that help you remember the products. If you buy Times Tales, the work is already done for you, and there are illustrations and flash cards and other helps. You can do the same thing yourself, though, with a little imagination.
For example: Draw a 5 and doodle it into a duck. Draw a 9 and turn it into a balloon with a string. Then make up a scenario, such as, "The duck had a balloon that blew away in the wind, and he chased it for 45 minutes." 5 x 9 = 45
Draw an 8 and turn it into an owl: "The owl saw the balloon stuck in a tree. He hopped across 7 branches and pecked it 2 times before it popped." 8 x 9 = 72.
Draw a 6 and make it into a mouse with a long tail. "The owl tried to catch the mouse but those 4 tiny feet ran 8 yards to his hole and he was safe," 6 x 8 = 48
Draw 7 and make it a flag. "The duck saluted the flag from 3pm to 5pm." 5 x 7 = 35
Anyway, you get the idea. You don't have to make up a story for all of them, just the ones your child finds hard to remember. If you can get your child to make up the scenarios, all the better!
Saturday, September 5, 2015
Solving Memorization Problems
What if I gave you the sign below and asked you to post it up on the wall-- but I didn't give you any tape? Or if I asked you to put it up on a bulletin board without tacks or staples, or on a refrigerator without a magnet? You could put that paper in the same place over and over, and it would never stay. No matter how many times you tried, it would fall to the ground every time.
Your child's memory can be that way, too. Have you seen your child practice those math facts over and over, and nothing seems to stick? Or maybe you've been helping her with those states and capitals, and she still can't remember that Concord is the capital of New Hampshire?
Your child can be very bright and still have trouble with these things. In fact, sometimes it is because your child is bright-- her brain is busy learning new concepts, thinking through ideas, making sense out of the world. It is busy making connections between one concept and another. And unfortunately, busy brains tend to discard what feels like random facts that are unconnected to anything else, no matter how many times they may be exposed to these facts. Endless repetition of flash cards or other drills, if they're not working, will only frustrate your child and drive you both insane.
What the brain needs is just what you needed when I gave you the sign-- something to make it stick. And that "something" is not the same for every brain-- some brains need tape, some need staples or pins, some need magnets-- some may need glue, Velcro, or putty! Metaphorically speaking, of course. Using the wrong something can be as effective as trying to stick that sign on the wall with a magnet. So if your child is getting discouraged over his failure to memorize something important, maybe it's time to try a different tactic.
Mnemonic devices ("a pattern of letters, ideas, or associations that assist in remembering something") are helpful for many students. The sign itself is an example-- using "PANDA" as an acronym for classroom supplies. Associations, the sillier the better, are among my favorite memory aids. A great product for learning multiplication facts through associations is Times Tales. This is a set of silly one-liner "stories" that introduce children to characters that represent numbers, and then present a situation for each multiplication fact that helps tie the numbers together. For example, 'Mrs Week (7) and Mrs Snowman (8) were in a car driving one mile over the speed limit (56). ' 7 x 8 = 56. And I love Yo, Sacramento -- a book that teaches states and capitals with the silliest pictures ever: I will never, ever forget the capital of New Hampshire after seeing the illustration of a Concorde jet being driven by a Nude Hamster!
Music is a great memorization tool for a lot of people. Audio Memory has been around for decades and has taught thousands of children everything from math and grammar to geography and history through songs. Back in the 70's we had Schoolhouse Rock-- now available on dvd or YouTube. In fact, there are countless math fact drills set to music-- in pop, rap, even country styles-- that can be found on YouTube. Same with states and capitals. After 25 years, I can still recall the countries and capitals of South America from this song. Even the quadratic formula from algebra class has several songs in its honor. You can Google just about anything that commonly has to be memorized and find a song for it: just type in (the thing you have to memorize) and "song." Like, "layers of the atmosphere song" or, for a real challenge, "periodic table song."
But songs don't work for everybody. Some students remember things best when they build, or draw, or in some other way interact with the information. Maybe working a map puzzle, or labeling a plastic-covered page with a dry erase marker, or matching up a set of cards, would help those states and capitals stick. Maybe linking all the pairs of numbers that add up to 10 or 12 or 16 with a set of Cuisenaire rods would help with addition and subtraction facts. Maybe creating models of molecules and breaking them into atoms to reassemble into new molecules is the key to acing that chemistry test.
The point is, if something isn't working for your child and she's given it a good, honest effort, it's probably the wrong approach. Like using a thumbtack on a refrigerator, it's not going to stick. Try something different!
Your child's memory can be that way, too. Have you seen your child practice those math facts over and over, and nothing seems to stick? Or maybe you've been helping her with those states and capitals, and she still can't remember that Concord is the capital of New Hampshire?
Your child can be very bright and still have trouble with these things. In fact, sometimes it is because your child is bright-- her brain is busy learning new concepts, thinking through ideas, making sense out of the world. It is busy making connections between one concept and another. And unfortunately, busy brains tend to discard what feels like random facts that are unconnected to anything else, no matter how many times they may be exposed to these facts. Endless repetition of flash cards or other drills, if they're not working, will only frustrate your child and drive you both insane.
What the brain needs is just what you needed when I gave you the sign-- something to make it stick. And that "something" is not the same for every brain-- some brains need tape, some need staples or pins, some need magnets-- some may need glue, Velcro, or putty! Metaphorically speaking, of course. Using the wrong something can be as effective as trying to stick that sign on the wall with a magnet. So if your child is getting discouraged over his failure to memorize something important, maybe it's time to try a different tactic.
Mnemonic devices ("a pattern of letters, ideas, or associations that assist in remembering something") are helpful for many students. The sign itself is an example-- using "PANDA" as an acronym for classroom supplies. Associations, the sillier the better, are among my favorite memory aids. A great product for learning multiplication facts through associations is Times Tales. This is a set of silly one-liner "stories" that introduce children to characters that represent numbers, and then present a situation for each multiplication fact that helps tie the numbers together. For example, 'Mrs Week (7) and Mrs Snowman (8) were in a car driving one mile over the speed limit (56). ' 7 x 8 = 56. And I love Yo, Sacramento -- a book that teaches states and capitals with the silliest pictures ever: I will never, ever forget the capital of New Hampshire after seeing the illustration of a Concorde jet being driven by a Nude Hamster!
Music is a great memorization tool for a lot of people. Audio Memory has been around for decades and has taught thousands of children everything from math and grammar to geography and history through songs. Back in the 70's we had Schoolhouse Rock-- now available on dvd or YouTube. In fact, there are countless math fact drills set to music-- in pop, rap, even country styles-- that can be found on YouTube. Same with states and capitals. After 25 years, I can still recall the countries and capitals of South America from this song. Even the quadratic formula from algebra class has several songs in its honor. You can Google just about anything that commonly has to be memorized and find a song for it: just type in (the thing you have to memorize) and "song." Like, "layers of the atmosphere song" or, for a real challenge, "periodic table song."
But songs don't work for everybody. Some students remember things best when they build, or draw, or in some other way interact with the information. Maybe working a map puzzle, or labeling a plastic-covered page with a dry erase marker, or matching up a set of cards, would help those states and capitals stick. Maybe linking all the pairs of numbers that add up to 10 or 12 or 16 with a set of Cuisenaire rods would help with addition and subtraction facts. Maybe creating models of molecules and breaking them into atoms to reassemble into new molecules is the key to acing that chemistry test.
The point is, if something isn't working for your child and she's given it a good, honest effort, it's probably the wrong approach. Like using a thumbtack on a refrigerator, it's not going to stick. Try something different!
Wednesday, August 26, 2015
Four Easy Reading/Writing Tips
Here are some common reading and writing problems and ways to work on them. The first two have to do with individual words, the last two with longer passages:
1) When a student reads aloud, he misreads words, substituting similar words, such as "medical" for "mechanical." Note how the words begin and end the same way-- the brain is tempted to fill in the middle with a word it already knows, especially if the actual word on the page is unfamiliar. The brain must be trained to look at the middle part, too.
The best way to do this is to have the student divide the word into syllables. This can be done on paper, underlining or drawing lines on the printed word: me/chan/i/cal. (Note: this is a good time to remind the student that ch can represent three sounds: Chocolate, Christmas, and Charlotte.) Using 3-D manipulative letters or tiles is especially helpful, because they move freely and the student can put the word together and apart easily. Even letters written on small squares of paper can be used. Alternatively, the word can be written whole and cut up into syllables. The important thing is that the student becomes so adept at breaking up the word physically that he begins to see the words that way, and breaks them up mentally without thinking.
2) When a student has to spell a long or difficult word, he may put in the wrong letters, or can't remember which letters are correct. Have him look at the word syllable by syllable. Practice with 3-D letters as explained above.
The preceding tips were for single-word errors; now, let's look at a couple of common problems students have when reading paragraphs or articles:
3) When a student is called upon to determine the main idea, or central idea, of a passage he is reading, he chooses a sub-point from the passage instead. The task is harder than it sounds, especially while the brain is still developing abstract thought. Students must not only read and comprehend the information, but they must mentally sort supporting details from over-riding themes.
To practice this, have students start with easy part-whole exercises, such as "Parts of a house" "roof" "wall" "window" "door" "foundation." If you have two identical pictures of a house, and cut one up, the student gets the idea quickly. Put the whole house picture at the top of the desk, and line the parts up below it. The idea is for the student to see that the "main idea" includes all of the supporting details. And each supporting detail is a part of the main idea.
Similarly, you could use "parts of an ice cream sundae" "ice cream" "chocolate sauce" "whipped cream" "nuts" "cherry," or "animals on the farm" "cow" "horse" "pig" "goat" "chicken." Then move on to words instead of pictures.
Finally, give your student a set of several entire sentences instead of words-- cut them into sentence strips and have your child find the one which works best as the main idea. Can you pick the main idea from this set?
If your student has trouble sorting the sentences, have her underline 3-4 key words from each sentence. This will help her focus on what each sentence is about. In this way, she can see that of the sentences above, most are about individual desert animals. Only one has the general "many animals" as its topic; this is the main idea that all the other more specific sentences fall into. Some students will need a lot of practice with this skill.
If the student is supposed to come up with the main idea on his own, or choose between a few given possibilities, have him write facts from the passage on sticky notes. Write possible "main idea" choices on a white board. See which main idea choice can have all facts fit underneath it.
Writing a cohesive paragraph requires the same understanding of main idea and supporting details. The only difference is that the student has to decide what details to include in order to support his main idea. So when your child can easily distinguish between main idea and supporting details, try giving him a set of main idea and supporting details with an added red herring-- an off-topic detail for him to identify and discard. For example, in the list above, an off-topic detail would be, "Dolphins prefer the warm waters of the Pacific Ocean." When he can find one, try giving him a set with more than one discardable detail. This will help him when he looks at his own writing. At that point, writing his thoughts on a graphic organizer such as one of these might help him develop his paragraph(s).
4) A student comprehends what he reads, but can't skim for information that he needs quickly. He doesn't change his reading speed whether he is reading for pleasure or for information. While most students have been taught to read through the questions on an assignment so they'll know what to look for in the text, they often don't realize that reading every word of the text is not always the best means of then finding that information. Sometimes they just need to know a certain fact. So they need to be able to focus their search logically. For example, if a student is looking through a passage for the answer to "How far is the earth from the sun?" ask her what are the most important words in the question. How far, earth, sun. What words might be in the answer? Earth, sun, and some number.
When the student understands that she is looking for a number and the words "earth" and "sun," she must then be able to skim efficiently through the passage, ignoring everything that isn't a number or those two words. Just as importantly, having found the words and/or a number, the student should be able to read the sentence they appear in to verify that it does indeed answer the question.
Skimming is an eye+brain discrimination skill, and takes practice. It is one of the skills honed in word searches and those 'hidden pictures' games we enjoyed as children. But there are ways to build proficiency; when the student knows she is looking for numbers, for example, she can try to underline all the numbers. That will help the brain focus. Also, when looking for a particular word, she can get a picture in her mind of what that word will look like. A good way to practice is to pick a page of a book at random and ask the child to find a specific word. Make it a word that is at least half-way down the page at first; then try other words that may be nearer the top or bottom of the page. The student should try to find it as fast as possible.
These four tips are not overnight game-changers, but with practice, can make a difference in how well your child reads and performs in school.
1) When a student reads aloud, he misreads words, substituting similar words, such as "medical" for "mechanical." Note how the words begin and end the same way-- the brain is tempted to fill in the middle with a word it already knows, especially if the actual word on the page is unfamiliar. The brain must be trained to look at the middle part, too.
The best way to do this is to have the student divide the word into syllables. This can be done on paper, underlining or drawing lines on the printed word: me/chan/i/cal. (Note: this is a good time to remind the student that ch can represent three sounds: Chocolate, Christmas, and Charlotte.) Using 3-D manipulative letters or tiles is especially helpful, because they move freely and the student can put the word together and apart easily. Even letters written on small squares of paper can be used. Alternatively, the word can be written whole and cut up into syllables. The important thing is that the student becomes so adept at breaking up the word physically that he begins to see the words that way, and breaks them up mentally without thinking.
2) When a student has to spell a long or difficult word, he may put in the wrong letters, or can't remember which letters are correct. Have him look at the word syllable by syllable. Practice with 3-D letters as explained above.
Careful correct pronunciation, or over-pronunciation, can be helpful in distinguishing which vowels to use. For example, "ridiculous" is easier to spell if you pronounce it as rid-ih-cu-lus instead of ree- dic-you-luss." “Difficult” is easier to spell if you say diff-ih-cult and not diff-uh-cult.
If a word is particularly tricky, mentally mispronouncing the word (phonetically) on purpose can help her remember how it is spelled. For instance, say "deter + MINE" instead of "deter + men." "Rendezvous" is easy to remember if you say it in your head as "rehn" "dez" "voos" instead of "ron" "day" "voo." "Perseverance" is easier to spell "per + sev + er + ance " but be careful not to say “enss” at the end.
The preceding tips were for single-word errors; now, let's look at a couple of common problems students have when reading paragraphs or articles:
3) When a student is called upon to determine the main idea, or central idea, of a passage he is reading, he chooses a sub-point from the passage instead. The task is harder than it sounds, especially while the brain is still developing abstract thought. Students must not only read and comprehend the information, but they must mentally sort supporting details from over-riding themes.
To practice this, have students start with easy part-whole exercises, such as "Parts of a house" "roof" "wall" "window" "door" "foundation." If you have two identical pictures of a house, and cut one up, the student gets the idea quickly. Put the whole house picture at the top of the desk, and line the parts up below it. The idea is for the student to see that the "main idea" includes all of the supporting details. And each supporting detail is a part of the main idea.
Finally, give your student a set of several entire sentences instead of words-- cut them into sentence strips and have your child find the one which works best as the main idea. Can you pick the main idea from this set?
- Tortoises and lizards, spiders and scorpions are desert inhabitants.
- Many animals make their home in the desert.
- The javelina, or peccary, enjoys the cactus fruit in late summer.
- Jack rabbits hide among the prickly pear.
- Snakes of many kinds roam the desert floor and sun themselves on rocks.
- Coyotes roam the desert in search of prey.
If your student has trouble sorting the sentences, have her underline 3-4 key words from each sentence. This will help her focus on what each sentence is about. In this way, she can see that of the sentences above, most are about individual desert animals. Only one has the general "many animals" as its topic; this is the main idea that all the other more specific sentences fall into. Some students will need a lot of practice with this skill.
If the student is supposed to come up with the main idea on his own, or choose between a few given possibilities, have him write facts from the passage on sticky notes. Write possible "main idea" choices on a white board. See which main idea choice can have all facts fit underneath it.
Writing a cohesive paragraph requires the same understanding of main idea and supporting details. The only difference is that the student has to decide what details to include in order to support his main idea. So when your child can easily distinguish between main idea and supporting details, try giving him a set of main idea and supporting details with an added red herring-- an off-topic detail for him to identify and discard. For example, in the list above, an off-topic detail would be, "Dolphins prefer the warm waters of the Pacific Ocean." When he can find one, try giving him a set with more than one discardable detail. This will help him when he looks at his own writing. At that point, writing his thoughts on a graphic organizer such as one of these might help him develop his paragraph(s).
4) A student comprehends what he reads, but can't skim for information that he needs quickly. He doesn't change his reading speed whether he is reading for pleasure or for information. While most students have been taught to read through the questions on an assignment so they'll know what to look for in the text, they often don't realize that reading every word of the text is not always the best means of then finding that information. Sometimes they just need to know a certain fact. So they need to be able to focus their search logically. For example, if a student is looking through a passage for the answer to "How far is the earth from the sun?" ask her what are the most important words in the question. How far, earth, sun. What words might be in the answer? Earth, sun, and some number.
When the student understands that she is looking for a number and the words "earth" and "sun," she must then be able to skim efficiently through the passage, ignoring everything that isn't a number or those two words. Just as importantly, having found the words and/or a number, the student should be able to read the sentence they appear in to verify that it does indeed answer the question.
Skimming is an eye+brain discrimination skill, and takes practice. It is one of the skills honed in word searches and those 'hidden pictures' games we enjoyed as children. But there are ways to build proficiency; when the student knows she is looking for numbers, for example, she can try to underline all the numbers. That will help the brain focus. Also, when looking for a particular word, she can get a picture in her mind of what that word will look like. A good way to practice is to pick a page of a book at random and ask the child to find a specific word. Make it a word that is at least half-way down the page at first; then try other words that may be nearer the top or bottom of the page. The student should try to find it as fast as possible.
These four tips are not overnight game-changers, but with practice, can make a difference in how well your child reads and performs in school.
Wednesday, August 12, 2015
Finding the fraction of a number (multiplying a whole number by a fraction)
When students are beginning to work with fractions, one concept they need to understand is that a fraction involves both division and multiplication at the same time. It's not as easy to see when using fraction bars or circles, because you're always starting with a fraction of a single thing-- a whole circle or a whole bar. It is not until you are trying to find the fraction of a whole number that you can see what's really going on.
In this demonstration, I am using pennies and a set of fraction squares that I made from clear plastic page protectors drawn on with permanent markers. I traced over a piece of graph paper to get my sections even (24 squares x 24 squares). The same effect could be obtained from squares of paper or drawn a whiteboard, as long as the student has a selection of fractions to choose from.
Now we use our model.
A) What is 1/2 of 12?
B) What is 2/3 of 12?
C) What is 3/4 of 12?
We start with 1/2 of 12, because the student will likely already know the answer, but can also show it with the model.
1. Choose the fraction block that matches the denominator in the problem. In this case, we are asked about 1/2, so we choose the square that is divided into 2 equal sections (halves).
2. Count out the correct number of pennies (or blocks or beads or whatever you're using) -- 12 in this problem-- and divide them evenly into the sections of the fraction square. In this case, six pennies go into each of the two sections.
3. Select the number of sections indicated by the numerator-- in this case, 1. Count the number of pennies in that/those section(s). So we see that 1/2 of 12 = 6.
To find two thirds of 12, we: 1. Choose the square divided into three equal sections (thirds). 2. Count out 12 pennies and place an equal number of them into each of the three sections of the square (4). 3. Select two of the sections and count the pennies in the sections. 2/3 of 12 = 8.
To find three fourths of 12, we: 1. Choose the square divided into four equal sections (fourths). 2. Count out 12 pennies and place an equal number of them into each of the four sections of the square (3). 3. Select three of the sections and count the pennies in the sections. 3/4 of 12 = 9.
Next, try different whole numbers with various fractions. Just be sure the whole number is always evenly divisible by the denominator in the fraction. For example, 3/5 of 15 would be a good practice problem, but we're not ready for 3/5 of 27.
After enough practice, the student should recognize that what she is doing is dividing the whole number by the denominator and then multiplying that product by the numerator. At this point, she can try using mental math to solve similar problems with larger whole numbers..
2/5 of 100 (40)
3/8 of 64 (24)
4/7 of 56 (32)
9/10 of 120 (108)
Finally, the student can be told that in math, "of" is generally translated "x" (multiplied by). So 2/5 of 100 is actually 2/5 x 100, and so on, for the rest of the problems.
In this demonstration, I am using pennies and a set of fraction squares that I made from clear plastic page protectors drawn on with permanent markers. I traced over a piece of graph paper to get my sections even (24 squares x 24 squares). The same effect could be obtained from squares of paper or drawn a whiteboard, as long as the student has a selection of fractions to choose from.
Now we use our model.
A) What is 1/2 of 12?
B) What is 2/3 of 12?
C) What is 3/4 of 12?
We start with 1/2 of 12, because the student will likely already know the answer, but can also show it with the model.
1. Choose the fraction block that matches the denominator in the problem. In this case, we are asked about 1/2, so we choose the square that is divided into 2 equal sections (halves).
2. Count out the correct number of pennies (or blocks or beads or whatever you're using) -- 12 in this problem-- and divide them evenly into the sections of the fraction square. In this case, six pennies go into each of the two sections.
3. Select the number of sections indicated by the numerator-- in this case, 1. Count the number of pennies in that/those section(s). So we see that 1/2 of 12 = 6.
To find two thirds of 12, we: 1. Choose the square divided into three equal sections (thirds). 2. Count out 12 pennies and place an equal number of them into each of the three sections of the square (4). 3. Select two of the sections and count the pennies in the sections. 2/3 of 12 = 8.
To find three fourths of 12, we: 1. Choose the square divided into four equal sections (fourths). 2. Count out 12 pennies and place an equal number of them into each of the four sections of the square (3). 3. Select three of the sections and count the pennies in the sections. 3/4 of 12 = 9.
Next, try different whole numbers with various fractions. Just be sure the whole number is always evenly divisible by the denominator in the fraction. For example, 3/5 of 15 would be a good practice problem, but we're not ready for 3/5 of 27.
After enough practice, the student should recognize that what she is doing is dividing the whole number by the denominator and then multiplying that product by the numerator. At this point, she can try using mental math to solve similar problems with larger whole numbers..
2/5 of 100 (40)
3/8 of 64 (24)
4/7 of 56 (32)
9/10 of 120 (108)
Finally, the student can be told that in math, "of" is generally translated "x" (multiplied by). So 2/5 of 100 is actually 2/5 x 100, and so on, for the rest of the problems.
Tuesday, August 11, 2015
Getting a perspective on decimals
In my years as a 6th grade teacher, I found many students who had trouble with decimal operations. They could read the numbers: "three hundred sixty-one and two hundredths," but then they'd get a problem such as 65.001 x 3.2 and come up with an answer like 2080.032, with no idea of why their answer made no sense. Addition, subtraction, and especially division all seemed quite hard. Their difficulty came because they didn't understand decimals enough to be able to estimate their answer to see if it made sense. For example, in the above problem, 65.001 might as well be plain old 65 and 3.2 is pretty close to 3, so the answer should be pretty close to 65 x 3. Even a ballpark estimate of 70 x 3 = 210 should tell the student that 2080.032 was way off.
It's easy for students to get confused about decimals, or even not understand the significance of where the decimal is placed. After all, when a decimal number is written, all the digits appear to be the same size and that little dot is awfully small-- surely it can't be that important! And for the many students who have trouble with whole number place value, the concept of decimal numbers can be almost meaningless.
So before introducing decimals, be sure your student has a firm grasp on place value. For example, in the number 222, the digits are the same, but their value is completely different. A student should understand that 222 is the same as 200 + 20 + 2. (Writing it this way is known as expanded notation, because the number is expanded into the digits' actual values.)
If a student can write a number in expanded notation, but still seems to have trouble keeping digits lined up when adding or subtracting, it might be helpful to use manipulatives. Here's a link to paper base ten blocks that can be cut out.
At left are some base 10 blocks (these are from the MathUSee basic set, but others work as well) illustrating what 222 looks like.
That's all fine and dandy, but what do you do to illustrate the relative size of decimal numbers?
One way is to use base ten blocks, only this time the largest block represents "one" and each smaller segment is a decimal number.
To match the previous set of base 10 blocks, I have made a giant "one" (out of paper and foam board) and colored it the same color as the original "one." It's as if the original one is being seen through a magnifying glass.
Here we see 2.222; notice the large blue "decimal" that matches the scale of the blocks.
Of course, the giant blocks don't match the scale of the original whole number blocks, so when you want to model what a whole number with decimals looks like, we have to go smaller. For this we can use modeling clay in a shade that matches the original "one" block. (If the student performs this activity himself, it may leave more of an impression, but either way it's one he'll remember.)
Here we see a "one" block and a block made of clay, approximately the same size.
Using a knife, cut the clay block in half, and then cut each half into 5 pieces. You have now divided one into tenths. Roll up each tenth into a ball.
Next, take one of the tenth balls and roll it into a snake that you can cut into ten tiny pieces. These are your hundredths. Roll them into little balls.
At this point, the student should begin to see just how different a hundredth is from a hundred!
It's almost impossible to divide the tiny hundredth ball into thousandths, so for the .001 place value, I use a pencil or marker of the same color to draw dots on the paper in the thousandths place. (White boards are a good base for this!)
Here you can barely see the pencil marks, but we have 0.222 illustrated.
Now, when we put the blocks all together, it is easy to see what 222.222 really looks like. At this point, it would be good to discuss with the student how significant the placement of the decimal point is.
And, of course, have the student practice writing and illustrating various numbers. Can he model 256.3? 256.03? 256.003? Which is bigger? Can he write the correct number when you place various numbers blocks in the columns?
Most importantly, can the student see why estimating with whole numbers can help him get the decimal placement right in his final answer? Those tiny little pieces of clay can be ignored long enough to get a ballpark idea of what the solution will be.
It's easy for students to get confused about decimals, or even not understand the significance of where the decimal is placed. After all, when a decimal number is written, all the digits appear to be the same size and that little dot is awfully small-- surely it can't be that important! And for the many students who have trouble with whole number place value, the concept of decimal numbers can be almost meaningless.
If a student can write a number in expanded notation, but still seems to have trouble keeping digits lined up when adding or subtracting, it might be helpful to use manipulatives. Here's a link to paper base ten blocks that can be cut out.
At left are some base 10 blocks (these are from the MathUSee basic set, but others work as well) illustrating what 222 looks like.
That's all fine and dandy, but what do you do to illustrate the relative size of decimal numbers?
One way is to use base ten blocks, only this time the largest block represents "one" and each smaller segment is a decimal number.
To match the previous set of base 10 blocks, I have made a giant "one" (out of paper and foam board) and colored it the same color as the original "one." It's as if the original one is being seen through a magnifying glass.
Here we see 2.222; notice the large blue "decimal" that matches the scale of the blocks.
Of course, the giant blocks don't match the scale of the original whole number blocks, so when you want to model what a whole number with decimals looks like, we have to go smaller. For this we can use modeling clay in a shade that matches the original "one" block. (If the student performs this activity himself, it may leave more of an impression, but either way it's one he'll remember.)
Here we see a "one" block and a block made of clay, approximately the same size.
Using a knife, cut the clay block in half, and then cut each half into 5 pieces. You have now divided one into tenths. Roll up each tenth into a ball.
Next, take one of the tenth balls and roll it into a snake that you can cut into ten tiny pieces. These are your hundredths. Roll them into little balls.
At this point, the student should begin to see just how different a hundredth is from a hundred!
It's almost impossible to divide the tiny hundredth ball into thousandths, so for the .001 place value, I use a pencil or marker of the same color to draw dots on the paper in the thousandths place. (White boards are a good base for this!)
Here you can barely see the pencil marks, but we have 0.222 illustrated.
Now, when we put the blocks all together, it is easy to see what 222.222 really looks like. At this point, it would be good to discuss with the student how significant the placement of the decimal point is.
And, of course, have the student practice writing and illustrating various numbers. Can he model 256.3? 256.03? 256.003? Which is bigger? Can he write the correct number when you place various numbers blocks in the columns?
Most importantly, can the student see why estimating with whole numbers can help him get the decimal placement right in his final answer? Those tiny little pieces of clay can be ignored long enough to get a ballpark idea of what the solution will be.
Wednesday, August 5, 2015
Subtraction: Borrowing, renaming, whatever you want to call it.
A fifth grader was having trouble with this problem:
The student knew there was borrowing, aka renaming, involved, because the top number ended in two 0's, and neither 1 nor 5 can be subtracted from 0. However, his method of renaming made me suspect he was unclear on just what was being renamed or borrowed from.
 |
| This was the student's solution. Can you spot two errors? |
Here we see the student has attempted to cover his bases by renaming the digits all the way across the top. He ends up with an incorrect answer, however, because the pattern he has learned is to turn zeroes into tens and subtract one from the digits on the left.
Using a whiteboard with colored markers, the student works through the problem. When he gets to the end, I call his attention to the hundreds column: did he need to borrow anything to subtract 3 from 7? No? Okay, so let's erase the 6. In fact, let's start over.
This time, I guide the student through the "borrowing" one step at a time:
1. Can 1 be subtracted from 0? No. We need to borrow from the left column to turn 0 into 10.
2. We can't borrow 1 from 0, but we CAN go one more column to the left and borrow 1 from 80. what is 80-1? It is 79. So we mark out the 80 and write 79 above it, then put the 1 above the last 0.
3. Now we start to subtract: 10-1= 9, 9-5= 4, 7-3= 4, 7- 0 = 7. Final answer: 7,449.
After a few times practicing with the whiteboard, it's time for a change of pace. So we build another problem with 3D letters. In this photo, we are using magnetic numbers on a paper-lined cookie sheet, and the paper has columns marked on it so we can line up the numbers correctly. (Try asking the student why the numbers need to be lined up carefully. What could happen if the top and bottom numbers were misaligned?)
This time, I guide the student through the "borrowing" one step at a time:
1. Can 1 be subtracted from 0? No. We need to borrow from the left column to turn 0 into 10.
2. We can't borrow 1 from 0, but we CAN go one more column to the left and borrow 1 from 80. what is 80-1? It is 79. So we mark out the 80 and write 79 above it, then put the 1 above the last 0.
3. Now we start to subtract: 10-1= 9, 9-5= 4, 7-3= 4, 7- 0 = 7. Final answer: 7,449.
After a few times practicing with the whiteboard, it's time for a change of pace. So we build another problem with 3D letters. In this photo, we are using magnetic numbers on a paper-lined cookie sheet, and the paper has columns marked on it so we can line up the numbers correctly. (Try asking the student why the numbers need to be lined up carefully. What could happen if the top and bottom numbers were misaligned?)
This time, we guide the student through the process:
1. In the ones column, you have 3 - 6. Is that doable? No, you must borrow from the tens column on the left.
2. The tens column has a zero! No tens to borrow; go left again.
3. The hundreds column has a zero! No hundreds to borrow; go left again.
4. The thousands column has a 5. Change it to 499+1 (4990 + 10), use the 10 to turn the 3 into a 13. Now subtraction can proceed.
By keeping all the digits within a column the same color, it becomes clear where the "1" is being borrowed from.
If the concept is still unclear, it may help to have the student perform the following exercise:
You'll need a box of 500-1000 craft sticks, a bag of 50 or more rubber bands, a large sheet of paper, a regular lined paper, and markers Prepare the sticks by bundling about 45 sets of ten sticks. Leave the rest loose. Then bundle 3 sets of 100 sticks by putting 10 sets of the 10-stick bundles together for each set of 100.
Prepare the large sheet of paper by folding it into three columns, and labeling the columns left to right, "hundreds," "tens," and "ones."
1. Give your student 364 sticks as pictured (3 hundreds, 6 tens, 4 singles.) Show her that each small bundle is 10 and the large bundles are 100.
2. Have her place the sticks on the sheet of paper in the appropriate columns.
3. Ask her how many sticks there are altogether. Have her write the number down on a separate sheet of lined paper (or a white board.)
4. Ask the student to write below 364, "-295."
5. Ask the student to take 295 sticks away from her collection of 364 to see what the result is.
If she starts by taking the 2 hundred bundles away, she'll be unable to complete the subtraction. She has to start with the ones.
When she starts by trying to take away 5 ones, she will not have enough ones. What is the solution? Borrow a 10 bundle. Now the 4 is 14. If she breaks apart the 10 bundle, she can take 5 from 14 and have 9 single sticks left over.
She now has 5 bundles of ten (50), but needs to subtract 9 (90). Solution? Borrow a hundreds bundle. Now she has 15 bundles of ten (150). When she separates the hundreds bundle, she can subtract 9 of them (90) and have 6 (60) left over.
She now has two hundreds bundles left over. When she subtracts those, there are none left. What she does have left is 6 bundles of ten and 9 singles, equalling 69.
5. Have the student work the problem on the lined paper, this time writing in the borrowed digits and marking out/changing the required donor digits. Her answer should again be 69.
With enough practice, the student should see the correlation between borrowing from the next highest bundle of sticks and borrowing from the digit on the left.
By keeping all the digits within a column the same color, it becomes clear where the "1" is being borrowed from.
If the concept is still unclear, it may help to have the student perform the following exercise:
You'll need a box of 500-1000 craft sticks, a bag of 50 or more rubber bands, a large sheet of paper, a regular lined paper, and markers Prepare the sticks by bundling about 45 sets of ten sticks. Leave the rest loose. Then bundle 3 sets of 100 sticks by putting 10 sets of the 10-stick bundles together for each set of 100.
Prepare the large sheet of paper by folding it into three columns, and labeling the columns left to right, "hundreds," "tens," and "ones."
1. Give your student 364 sticks as pictured (3 hundreds, 6 tens, 4 singles.) Show her that each small bundle is 10 and the large bundles are 100.
2. Have her place the sticks on the sheet of paper in the appropriate columns.
3. Ask her how many sticks there are altogether. Have her write the number down on a separate sheet of lined paper (or a white board.)
4. Ask the student to write below 364, "-295."
5. Ask the student to take 295 sticks away from her collection of 364 to see what the result is.
If she starts by taking the 2 hundred bundles away, she'll be unable to complete the subtraction. She has to start with the ones.
When she starts by trying to take away 5 ones, she will not have enough ones. What is the solution? Borrow a 10 bundle. Now the 4 is 14. If she breaks apart the 10 bundle, she can take 5 from 14 and have 9 single sticks left over.
She now has 5 bundles of ten (50), but needs to subtract 9 (90). Solution? Borrow a hundreds bundle. Now she has 15 bundles of ten (150). When she separates the hundreds bundle, she can subtract 9 of them (90) and have 6 (60) left over.
She now has two hundreds bundles left over. When she subtracts those, there are none left. What she does have left is 6 bundles of ten and 9 singles, equalling 69.
5. Have the student work the problem on the lined paper, this time writing in the borrowed digits and marking out/changing the required donor digits. Her answer should again be 69.
With enough practice, the student should see the correlation between borrowing from the next highest bundle of sticks and borrowing from the digit on the left.
Subscribe to:
Comments (Atom)