Singapore math diagrams: word problems you can see

I was looking at a word problem this week, and the operation that I knew I was supposed to do on it just didn't look right.  The problem went something like this:

Betty crocheted 5/6 of a blanket, then her cat came along and unraveled 3/5 of what she had done.  What part of the whole blanket did the cat undo?

I knew this was a multiplication problem, but it just didn't feel right-- I couldn't see the logic of what was happening.  I know "of"-- as in 3/5 "of"  5/6 -- generally translates to multiplication, but my comprehension broke down somewhere between having 5/6 and then talking about the whole blanket.  Happily, I have years of experience using Singapore math models, so I knew exactly how to draw it out so I could make it make sense.

One of the strengths of Singapore math is that students use models to work a problem.  With these models, even young, concrete-thinking children are able to solve problems that normally require the use of algebra or complicated algorithms.

Here's how it works:

1. Betty crocheted 5/6 of a blanket   Draw a bar that represents the blanket and divide it into 6 pieces.

Now identify the part that was crocheted.

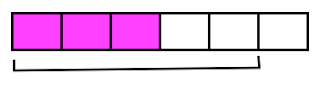
2. ...then her cat came along and unraveled 3/5 of what she had done.  

Looking at the bracketed sections, we notice there are five.  So 3/5 of the five sections is three sections, which we color in:

3. What part of the whole blanket did the cat undo?

Now it's fairly obvious that the cat unraveled half of the whole blanket.

So, now I can go back to the original problem and see if multiplication gives us the same answer:

Hooray!  It does-- 15/30  reduces to 1/2  (or by cross-reducing in the first place, I would have ended up with 1/2 right off.)  So multiplication was the way to go, whether it made sense at first or not.

Another example, one that would normally require algebra, might go something like this:

Betty has twice as many cookies as Freya had last night.  This morning, Freya ate five of her cookies, but Betty ate none.  Now, Betty has four times as many cookies as Freya.  How many cookies does Betty have?

So, again, we start with a bar.

We can model the first sentence like this:

Betty has twice as many cookies as Freya had last night. 

Here, the top divided bar represents the number of Betty's cookies. The bottom bar represents Freya's cookies.  We draw a line in the middle of Betty's bar, exactly in line with the end of Freya's bar,  to show that it is twice the value of Freya's.

We can color in Freya's bar or leave it blank.





The next two sentences go together:

This morning, Freya ate five of her cookies, but Betty ate none.  
Now, Betty has four times as many cookies as Freya.

Betty's bar is still the same size, because she still has the sam number of cookies.  But now we divide it into four equal pieces to show that it is four times the number of Freya's current number of cookies.

We keep Freya's bar the same size, to show what she started with.  But now, we use the 1/4 piece of Betty's bar to measure what's left of Freya's cookies.  Here, we colored in the remaining value for Freya's cookies.  And since we know that Freya ate 5 of her cookies, we know that the difference between the original length of Freya's bar and the new length is 5.

Since we see by the diagram that the 5 cookies turned out to be half of Freya's original amount of cookies, we can fill in each segment with the quantity of 5.

So, Betty has 20 cookies!


To solve this algebraically, we would have done something like this:

Betty has twice as many cookies as Freya had last night.  This morning, Freya ate five of her cookies, but Betty ate none.  Now, Betty has four times as many cookies as Freya.  How many cookies does Betty have?

F = the number of Freya's cookies.
B = the number of betty's cookies


Betty has twice as many cookies as Freya had last night.     B = 2F

This morning, Freya ate five of her cookies, but Betty ate none.  
Now, Betty has four times as many cookies as Freya.                          4(F-5) = B


And solve for F by substitution:  

2F = 4(F-5)
2F = 4F - 20
2F-4F = 4F-4F - 20
-2F = -20
-2F/-2 = -20/-2
F = 10

Then solve for B:

B = 2F
B = 2(10)
B = 20

Yeah, I'm liking those math diagrams!

Finding the fraction of a number (multiplying a whole number by a fraction)

When students are beginning to work with fractions,  one concept they need to understand is that a fraction involves both division and multiplication at the same time.  It's not as easy to see when using fraction bars or circles, because you're always starting with a fraction of a single thing-- a whole circle or a whole bar.  It is not until you are trying to find the fraction of a whole number that you can see what's really going on.

In this demonstration, I am using pennies and a set of fraction squares that I made from clear plastic page protectors drawn on with permanent markers.  I traced over a piece of graph paper to get my sections even (24 squares x 24 squares).  The same effect could be obtained from squares of paper or drawn a whiteboard, as long as the student has a selection of fractions to choose from.

Now we use our model.

A) What is 1/2 of 12?
B) What is 2/3 of 12?
C) What is 3/4 of 12?

We start with 1/2 of 12, because the student will likely already know the answer, but can also show it with the model.

1. Choose the fraction block that matches the denominator in the problem.  In this case, we are asked about 1/2, so we choose the square that is divided into 2 equal sections (halves).

2. Count out the correct number of pennies (or blocks or beads or whatever you're using) -- 12 in this problem-- and divide them evenly into the sections of the fraction square.  In this case, six pennies go into each of the two sections.

3. Select the number of sections indicated by the numerator-- in this case, 1.  Count the number of pennies in that/those section(s).  So we see that 1/2 of 12 = 6.

To find two thirds of 12, we: 1. Choose the square divided into three equal sections (thirds).  2. Count out 12 pennies and place an equal number of them into each of the three sections of the square (4).  3. Select two of the sections and count the pennies in the sections.  2/3 of 12 = 8.

To find three fourths of 12, we: 1. Choose the square divided into four equal sections (fourths).  2. Count out 12 pennies and place an equal number of them into each of the four sections of the square (3).  3. Select three of the sections and count the pennies in the sections.  3/4 of 12 = 9.

Next, try different whole numbers with various fractions.  Just be sure the whole number is always evenly divisible by the denominator in the fraction.  For example, 3/5 of 15 would be a good practice problem, but we're not ready for 3/5 of 27.

After enough practice, the student should recognize that what she is doing is dividing the whole number by the denominator and then multiplying that product by the numerator.   At this point, she can try using mental math to solve similar problems with larger whole numbers..

2/5 of 100 (40)
3/8 of 64 (24)
4/7 of 56 (32)
9/10 of 120 (108)

Finally, the student can be told that in math, "of" is generally translated "x" (multiplied by).  So 2/5 of 100 is actually 2/5 x 100, and so on, for the rest of the problems.

Multiplying vs dividing by fractions: Let's Make Brownies!

Multiplying or dividing fractions by a whole number is pretty easy to demonstrate.  Multiplying and dividing fractions BY fractions, however, can be a confusing business!  The algorithms aren't so bad-- to multiply one fraction by another, simply multiply across the top (numerators) and then across the bottom (denominators), reducing the end result when possible:

Division works the same way, except that the second fraction is "flipped" (inverted) before multiplying:

The typical textbook fraction multiplication model involves shading a rectangle with one fraction horizontally and shading the other fraction vertically.  The intersection is the solution.  That's fine.

1/2 x 2/3 =1/3

Here we have the vertical fraction, 1/2, shaded in pink, and the horizontal fraction, 2/3, shaded in black.  The place where they overlap is the solution-- 2/6 of the rectangle, or 1/3.

Division modeling gets a little trickier.  To model 1/2 ÷ 2/3, you have to show how many 2/3's are in 1/2-- which is not even one, but another fraction.

This lovely box diagram shows 1/2 of the box shaded in pink, and then 2/3 of the box shaded in black.  This time, both fractions are shaded in the same direction (here, vertically).  Again, the overlapping shading gives us the solution-- the difference here is that the overlapped part is measured in terms of the black shaded section-- the overlapped part covers 3/4 of the black shaded area. 

The difference in division modeling is also obvious when the dividend fraction is divided by a smaller divisor fraction.

In this case, the shaded 1/2 section is being divided by the outlined 1/6.  How many 1/6 are in 1/2?  There are three.

Not surprisingly, many students still don't understand what it is they're actually doing when they're multiplying or dividing fractions, so translating it into word problems can be frustrating.  To make the concepts clear, all you need is a fresh-baked batch of brownies, some measuring cups, and maybe some paper and scissors.

First, bake the brownies.  Then, consider this problem:

John made a pan of brownies and shared them with his friends.   They ate half of the brownies in the pan.  After they left, Dad ate two thirds of the remaining brownies.  How much of the original batch did Dad eat?

Is this a multiplication or a division problem?

To help your child understand what's going on, she needs to know two things:

1) The multiplication sign can generally be translated "of" in English.  2x100 means two (sets) of 100, which is 200.  1/2 x 100 means one half of 100, which is 50.

2) Division answers the question, "How many (sets of) _the second number_  are in _the first_?"  100 ÷ 50 is asking, How many sets of 50 are in 100? = 2.  50 ÷ 1/2  asks,  "How many sets of 1/2 are in 50? = 100.

So, back to the brownies-- if we have half a pan of brownies and Dad eats 2/3 OF those,  we can figure out how much Dad ate by multiplying.  1/2 x 2/3 = 1/3.  Dad ate a third of the original batch!

Obviously, to model this with brownies, you'll have to cut the brownies into six even pieces, eat half of them, and then put two thirds of the remainder onto a plate, to see that what's going on the plate is 1/3 of the original pan.

Here is half of the pan of brownies. (Of course, these could also be cookie bars,  rice cereal bars, even gelatin "jigglers," depending on what your students are allowed to eat.)

Here is the 2/3 of the remaining half.  Note that it can also be described as 2/6, but since 2/6 = 1/3, our final answer is 1/3.








So, what would a division word problem look like?  Try this:

John has a recipe for brownies that calls for 1/3 cup of cocoa per batch.  There is 3/4 cup of cocoa in the box.  How many batches of brownies can he make with the cocoa he has?

In this case, we want to know how many sets of 1/3 are in 3/4?  So we divide:

So, John has enough cocoa to make two full batches of brownies and 1/4 of another batch.

A less high-calorie method of modeling fractions is to use measuring cups with water or dry rice. For example, you can measure out 3/4 cup ofto your heart's content. rice, and see how many times you can fill 1/3 cup with that amount.  You will show that 3/4 cup can be divided by 1/3 cup twice, with one fourth of the 1/3 cup left over-- that is, there are 2 1/4 sets of 1/3 cup in 3/4 cup.   Similarly, you can measure out 2/3 cup 1/3 cup of rice, divide it in half and show that the half amount fills a single cup: 1/2 x 2/3 = 1/3.

Another way to model the fractions is by using paper fraction strips.  Print out as many as you need, and then you can model "half of 2/3" (1/2 x 2/3 = 1/3) or "how many 1/4's in 6/8" (6/8 ÷ 1/4 = 3). More on that on a future post.